Практически все ученые в своих исследованиях, статьях или диссертациях используют при теститровании статистических гипотез показатель P-значение (англ. P-value). Фактически — это вероятность ошибки при отклонении нулевой гипотезы (ошибки первого рода). Проверка гипотез с помощью P-значения является альтернативой классической процедуре проверки через критическое значение распределения.
Обычно P-значение равно вероятности того, что случайная величина с данным распределением (распределением тестовой статистики при нулевой гипотезе) примет значение, не меньшее, чем фактическое значение тестовой статистики.
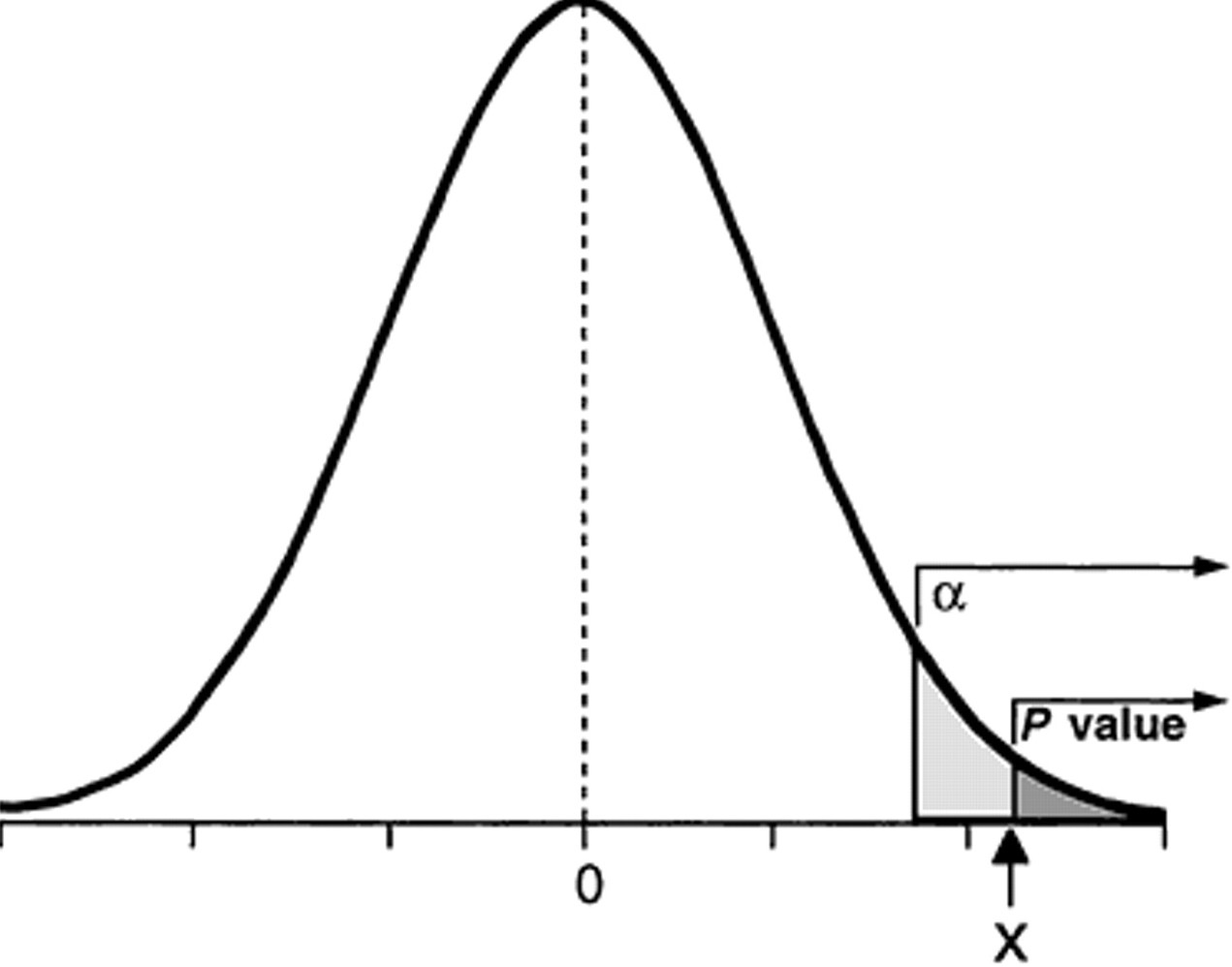
Пару слов из теории статистики.
Статистика делится на описательную и аналитическую. Задача аналитической статистики — предоставить методы, с помощью которых можно было бы объективно выяснить, например, является ли наблюдаемая разница в средних значениях или взаимосвязь (корреляция) выборок случайной, или нет.
Если сравниваются два средних значения выборок, то можно сформулировать две предварительные гипотезы:
- Гипотеза 0 (нулевая): Наблюдаемые различия между средними значениями выборок находятся в пределах случайных отклонений.
- Гипотеза 1 (альтернативная): Наблюдаемые различия между средними значениями нельзя объяснить случайными отклонениями.
В аналитической статистике разработаны методы вычисления, так называемых тестовых (контрольных) величин, которые рассчитываются по определенным формулам на основе данных, содержащихся в выборках или полученных из их характеристик. Эти тестовые величины соответствуют определенным теоретическим распределениям (t-pacnpeлелению, F-распределению, распределению X2 и т.д.), которые позволяют вычислить, так называемую, вероятность ошибки. Эта вероятность равна проценту ошибки, которую можно допустить отвергнув нулевую гипотезу и приняв альтернативную.
Вероятность определяется в математике, как величина, находящаяся в диапазоне от 0 до 1. В практической статистике она также часто выражается в процентах (%). Обычно вероятность обозначаются буквой р:
0 < р < 1
Вероятность ошибки, при которой допустимо отвергнуть нулевую гипотезу и принять альтернативную гипотезу, зависит от каждого конкретного случая. В значительной степени эта вероятность определяется характером исследуемой ситуации. Чем больше требуемая вероятность, с которой надо избежать ошибочного решения, тем более узкими выбираются границы вероятности ошибки, при которой отвергается нулевая гипотеза, так называемый доверительный интервал вероятности. Наиболее часто в исследованиях используют вероятность ошибки 0,05 (5%).
Существует общепринятая терминология, которая относится к доверительным интервалам вероятности:
- Вероятность ошибки р <= 0,05 — называется значимой.
- Вероятность ошибки р <= 0,01 — очень значимой,
- Вероятность ошибки р <= 0,001 — максимально значимой.
В литературе такие ситуации иногда обозначают одной, двумя, тремя, или четырьмя звездочками. Три и четыре звездочки – максимально значимая вероятность ошибки. В SPSS вероятность ошибки р имеет различные обозначения; звездочки для указания степени значимости применяются лишь в немногих случаях. Обычно в SPSS значение р обозначается Sig. (Significant).
Заключения, по имеющимся отклонениям на уровне ошибки p-value, не всегда отражают реальную картину.
Так как многие исследователи используют показатель p-value в своих работах, в своей практике они наблюдают расхождения в экспериментальном использовании значения p и причинно-следственных связях, которые они выявляют.
Поэтому при использовании p-value, надо иметь ввиду:
- Факт значимой взаимосвязи двух переменных ничего не говорит нам о причинах и следствиях. Дело в том, что группировка статистических показателей может быть собрана по разному, и сами статистические группы могут быть организованы по разному.
- Выявленные причинно-следственные связи первичны, значения p-value – вторичны (они могут подтвердить причинно-следственные связи, могут с ними расходиться). Только исследователь решает, необходимы дополнительные исследования, или нет.
- Например, статистическая значимость 0.04 — это вероятность близка к привычным 5%, которые чаще всего используют исследователи. Но 0.04 может не отражать разброс всех данных. И только многочисленные отклонения в трендах, которые и должен задавать исследователь, чтобы приблизиться к истине, представляют исследователю больше данных для анализа. Истина, как я указывала выше, кроется в причинно-следственных связях, а 0.04, как в нашем примере, надо рассматривать как дополнительные характеристики для обоснования вашей гипотезы.
Обеспокоенность по использованию p-value рассматривается учеными. И это радует, так как обоснование научных исследований часто превращаются в «механические расчеты», по которым далеко не всегда живет природа и сама наука.
Международная обеспокоенность.
Обеспокоенность по поводу широко распространенного недопонимания и ненадлежащего использования p-значений в науке побудила Американскую статистическую ассоциацию (ASA) опубликовать в 2016 году свое первое в истории заявление о правильном использовании статистического инструмента, в нем 6 принципов.
Например, определение, что научные выводы не должны основываться только на p-значении. «Практика, которая сокращает анализ данных или научный вывод до механических правил» (таких как p <0,05) для обоснования научных утверждений или выводов, может привести к ошибочным убеждениям и плохому принятию решений», — говорится в заявлении ASA. «Вывод не сразу становится «верным» с одной стороны и «ложным» — с другой». Заявление ASA также указывает на то, что, возможно, p-value является самым большим заблуждением в науке.
Подытожим. Резюме.
Использование дополнений p-value к другим статистическим данным, таким как доверительные интервалы, может лучше учитывать обоснованность гипотезы.
Добавление большего количества статистических слоев не решает проблемы скрытой множественности и избирательных искажений отчетности.
Прозрачность имеет важное значение. Ваши методы, способы исследования, а также схемы исследования и результаты должны быть прозрачны, и они могут иметь больше возможностей в доказательной базе, чем оценка p-value.
Распространенным заблуждением среди не статистов является то, что p-value может доказать нам вероятность того, что результат произошел случайно.
Значение p только говорит нам, что-то о вероятности того, что ваши результаты будут получены при конкретном гипотетическом объяснении — оно не может открыть вам вероятность того, что результаты истинны, или они являются случайными.